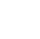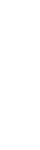Un conjunto es grupo de cosas que tienen algo en común, eso que tiene en común es una característica que los define como parecidos o similares. Otra definición de conjunto es decir que toda colección de cosas comunes es un conjunto. Las cosas que forman un conjunto se les denomina elementos del conjunto.
Existen dos formas de determinar un conjunto, por extensión y por compresión.
Decimos que un conjunto se determinar por extensión cuando se conocen y se da una lista de todos y cada uno de los elementos de un conjunto.
Ejemplo 1.
Determinar por extensión, el conjunto de los días de la semana.
Este conjunto estará constituido por los siguientes elementos: Lunes, Martes, Miércoles, Jueves, Viernes, Sábado, Domingo. Y su representación simbólica es:
S = { Lunes, Martes, Miércoles, Jueves, Viernes, Sábado, Domingo }
Siempre en la representación simbólica se usan letras mayúsculas para identificar el conjunto, y los elemento se encierran con llaves {} y separados por comas.
Ejemplo 2.
El conjunto de todos los números naturales menores que 10.
Este conjunto estará constituido por los siguientes elementos: 1, 2, 3, 4, 5, 6, 7, 8, 9. Y su representación simbólica es:
M = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
Decimos que un conjunto se determina por compresión cuando se describe una o varias características o propiedades que lo define, y no se da una lista de cada uno de sus elementos.
Ejemplo 1.
Determinar por compresión el conjunto de los días de la semana.
Al determinar por compresión el conjunto, la propiedad será la frase : “un día de la semana”. Y simbólicamente su representación será:
S = { x : x es un día de la semana }
en donde x:x se debe leer como “x tal que x ”, a veces se suele cambiar el símbolo : por la barra invertida. del siguiente modo:
S = { x/x es un día de la semana }
Ejemplo 2.
Determinar por compresión el conjunto de los números naturales menores que 10.
Al determinar por compresión el conjunto, la propiedad se puede expresar a través de una desigualdad “n < 10”, y también por otra propiedad que nos indique que son sólo números naturales, como la siguiente: x ∈
. Simbólicamente tenemos:
M = { x/x ∈
en donde x/x ∈
Considere el conjunto de las vocales:
V = { a, e, i, o, u }
podemos observar que la letra "a" se encuentra dentro del conjunto de las vocales, entonces diremos que la letra "a" pertenece al conjunto de las vocales y se simboliza de la siguiente forma.
a ∈ V
Ahora consideremos la letra "d", de ello podemos observar que esta no se encuentra dentro del conjunto de las vocales, entonces diremos que la letra "d" no pertenece al conjunto de las vocales y se simboliza de la siguiente forma:
d ∉ V
La representación gráfica de un conjunto se hace con los diagramas de Venn, estos diagramas llamados así en honor a su creador el matemático, John Venn matemático y filosofo británico. Los diagramas de Venn pueden ser representados por la enumeración de sus elementos o por una o varias características o propiedades que lo identifica inequívocamente.
Para su representación por la enumeración de sus elementos, los elementos que pertenecen a un conjunto se encierran con líneas curvas cerradas, y por fuera se escribe la letra mayúscula que identifica al conjunto.
Ejemplo 1.
Representar gráficamente el conjunto A = { 0, 1, 2, 3, 4, 5 }
La representación gráfica del conjunto A = { 0, 1, 2, 3, 4, 5 } que también se puede definir por compresión como A = { x : x ∈
Para su representación por una o varias características que lo identifica inequívocamente, se suele hacer de varias maneras, una de ellas es dibujar el conjunto sin elementos pero indicando la propiedad o característica que lo define y en algunos casos pintando el interior del conjunto con un color que ayude a su definición. Este tipo de diagramas generalmente se usan para representar conjuntos en donde sus elementos resultan un tanto difícil de enumerar o también para representar conceptos.
Ejemplo 2.
Representar gráficamente el conjunto A = { x/x es un grano de arena }
La representación gráfica del conjunto A = { x/x es un grano de arena }, se puede representar del siguiente modo:
A = {x/x es un grano de arena}
Esta relación aparece cuando se puede observar que todos los elementos de un conjunto pertenecen a otro conjunto, entonces se dice que el primero es subconjunto del segundo o que está incluido en el segundo.
Ejemplo 1.
Sea el conjunto A de los números naturales menores que 10 y mayores que 0, el conjunto B todo los números divisibles con 2 o pares menores que 10 y el conjunto V = { 1, 3, 10, 11, 12 }. Determinar y graficar, si el conjunto B y V, están incluidos en A.
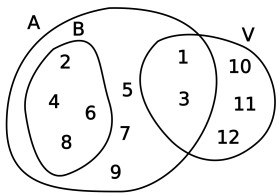
Deteminamos el conjunto de los números naturales menores que 10, A = { 1, 2, 3, 4, 5, 6, 7, 8, 9 } y el conjunto de todos los números divisibles con 2 o pares menores que 10, B = { 2, 4, 6, 8}. De esto se puede observar lo siguiente: Que todos los elementos del conjunto B pertenecen al conjunto A, entonces el conjunto B esta incluido en A, simbólicamente se escribe:
B ⊂ A
Pero no todos los elementos del conjunto V pertenecen al conjunto A, entonces se dice que el conjunto V no esta incluido en el conjunto A, simbólicamente se escribe:
V ⊄ A
Y su representación gráfica con los diagramas de Venn, de estos conjuntos se hace del siguiente modo:
Se dice que dos conjuntos son iguales, cuando los elementos de un conjunto también pertenecen al otro conjunto con el que se compara o se relaciona. Es decir, los elementos del conjunto A pertenecen al conjunto B. Otra forma de decir que dos conjuntos son iguales, es cuando el primer conjunto esta incluido en el segundo y el segundo también esta incluido en el primero, esta última definición de igualdad de conjuntos se puede expresar simbólicamente del siguiente modo:
A=B ↔ A⊂B y B⊂A
Ejemplo 1.
Dados los siguientes conjuntos, A = { 1, 2, 3, 4} y B = { x/x ∈
Se dice que ambos son iguales ya que todos los elementos de A, también pertenecen a B y viceversa todos los elementos de B también pertenecen a A.